Vehicle routing problems, crucial to modern urban transportation and logistics systems, require complex modern optimization algorithms and a vast amount of computational resources. KAIST researchers have developed a new machine-learning-based algorithm that significantly outperforms traditional methods, demonstrating the potential to find exact optimal solutions and reduce computing time in large-scale vehicle routing problems.

With the rapid rise of e-commerce, same-day delivery, and shared mobility, the diverse variants of vehicle routing problems (VRPs) pose challenges for urban transportation and logistics systems. VRPs are NP-hard combinatorial optimization problems that determine which customer (order or request) is served by which vehicle (driver or deliverer) in what order, as illustrated in Figure 1. The applications of VRPs include delivery of goods such as mail, parcels, food, and fresh produce, as well as mobility services for people such as school bus routing, carpooling, and demand-response transit problems.

Figure 1. Vehicle Routing Problem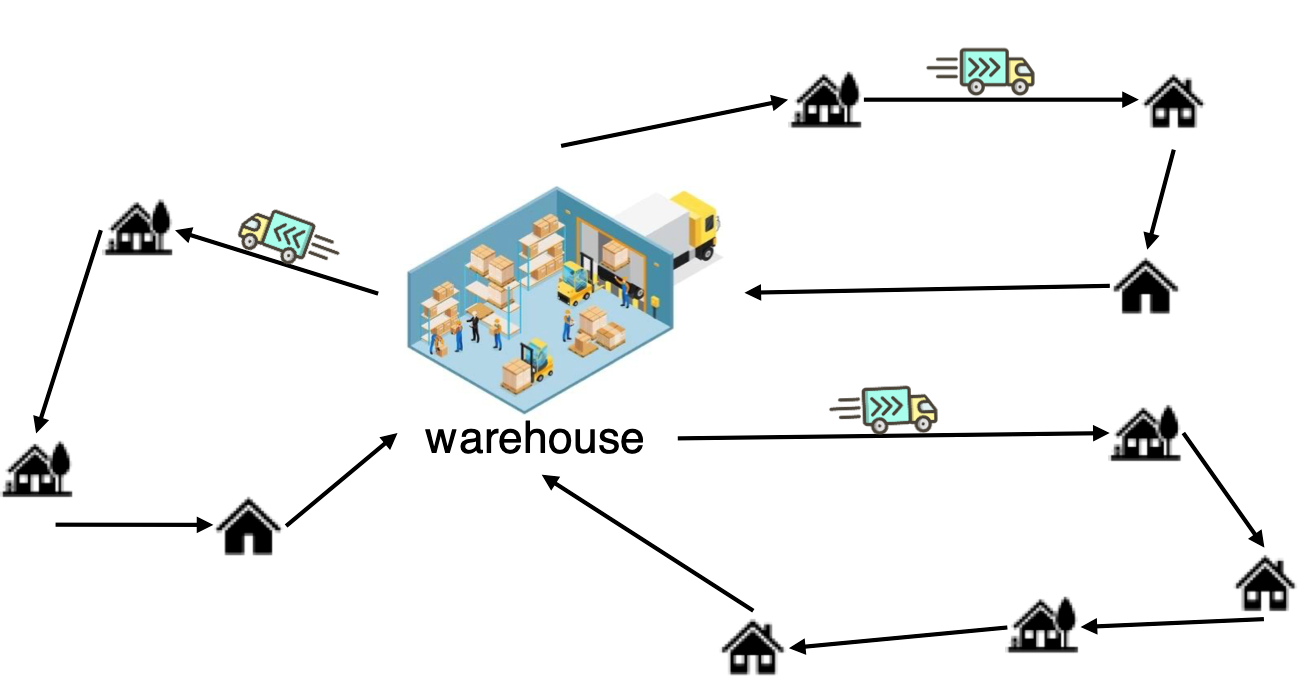

Modern mathematical optimization algorithms for VRPs, the branch-cut-and-price algorithms, consist of various components, some of which are based on solid mathematical theory, while some components are based on human-developed heuristic ideas. Both parts contribute to finding exact optimal solutions within the branch-cut-and-price framework. A critical component in most exact optimization algorithms is the identification of cutting planes, which help reduce the search space and find integer feasible solutions. To identify cutting planes, cut separation problems need to be solved.

In general, cut separation problems are NP-hard problems, and therefore, heuristic algorithms have been used. Researchers in the Department of Industrial and Systems Engineering at KAIST have developed a machine-learning-based algorithm that can outperform the most popular heuristic algorithm available currently. The new algorithm learns from optimal solutions in small-scale training instances and transfers learned algorithms to large-scale instances via message-passing graph neural networks and graph coarsening techniques.

Figure 2 compares the popular heuristic algorithm (CVRPSEP) with the new algorithm (NeuralSEP). The smaller the optimality gap is, the better the solution quality is. For the largest size of the problems with 1,000 customers, NeuralSEP significantly outperforms CVRPSEP, which can save hours and days of computing time in the entire branch-cut-and-price algorithm.

Figure 2. The range of optimality gap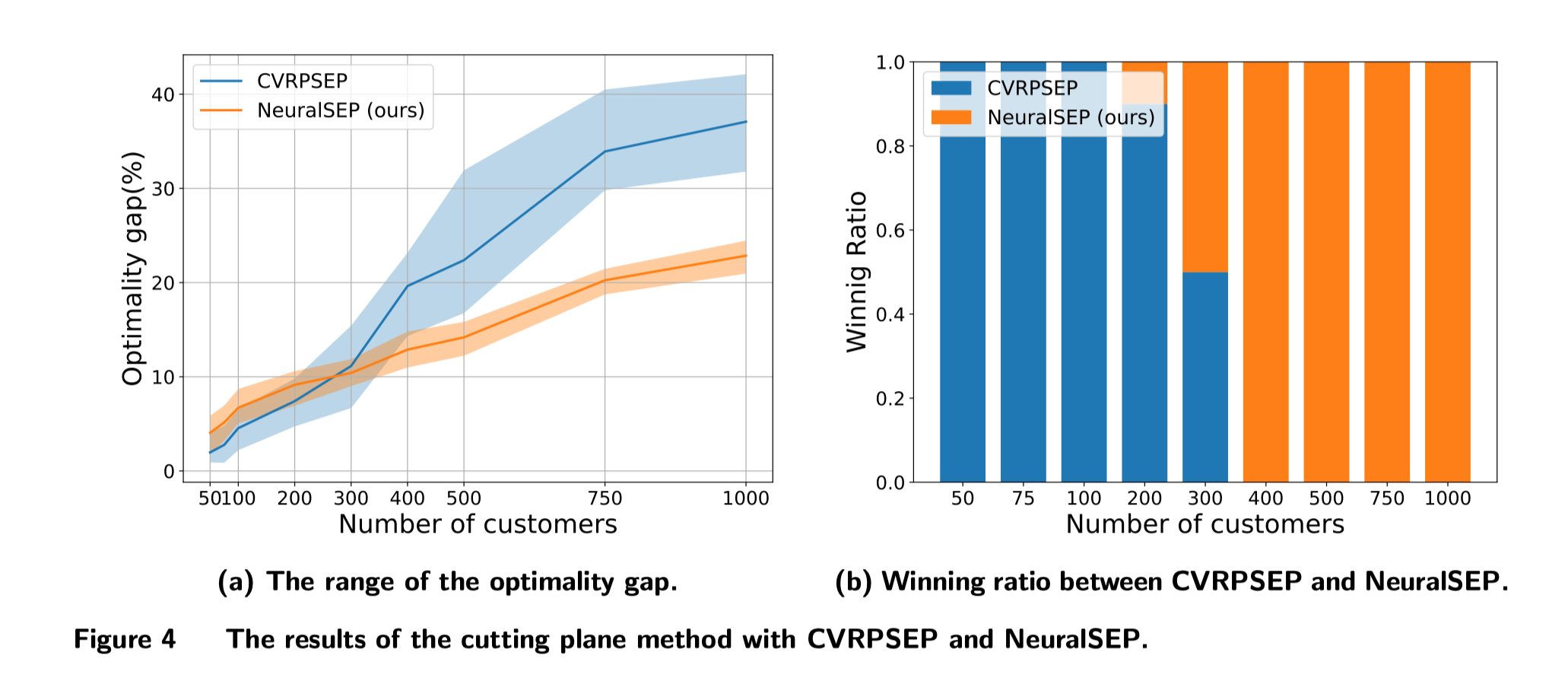

A full manuscript describing this research is available at: https://arxiv.org/abs/2306.17283.